Here is the original blog post.
Edit: Sorry, I can't get embedded LaTeX to display properly.
The pinned tutorial post says I have to do it in plain HTML without embedded images?
I actually tried embedding pre-rendered equations and they seemed fine when editing, 
but once I submit the post it just turned into a huge mess.
So...until I can find a proper way to fix this, please refer to the original blog post for formatted formulas.
I've replaced the original LaTex mess in this post with something at least more readable.
Any advice on fixing this is appreciated.

This post is part of my Game Math Series.

Source files are on GitHub.
Shortcut to sterp implementation.
Shortcut to code used to generate animations in this post.

An Alternative to Slerp

Slerp, spherical linear interpolation, is an operation that interpolates from one orientation to another, using a rotational axis paired with the smallest angle possible.

Quick note: Jonathan Blow explains here how you should avoid using slerp, if normalized quaternion linear interpolation (nlerp) suffices. Long store short, nlerp is faster but does not maintain constant angular velocity, while slerp is slower but maintains constant angular velocity; use nlerp if you’re interpolating across small angles or you don’t care about constant angular velocity; use slerp if you’re interpolating across large angles and you care about constant angular velocity. But for the sake of using a more commonly known and used building block, the remaining post will only mention slerp. Replacing all following occurrences of slerp with nlerp would not change the validity of this post.

In general, slerp is considered superior over interpolating individual components of Euler angles, as the latter method usually yields orientational sways.

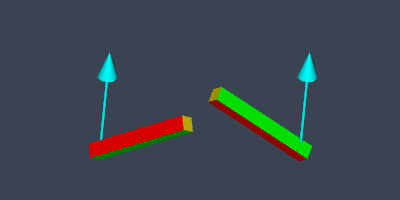
But, sometimes slerp might not be ideal. Look at the image below showing two different orientations of a rod. On the left is one orientation, and on the right is the resulting orientation of rotating around the axis shown as a cyan arrow, where the pivot is at one end of the rod.

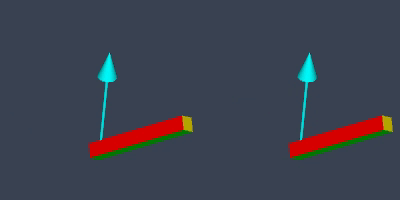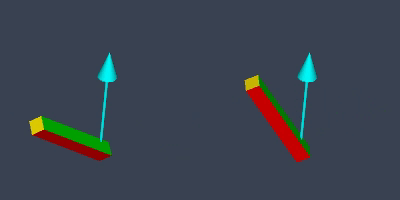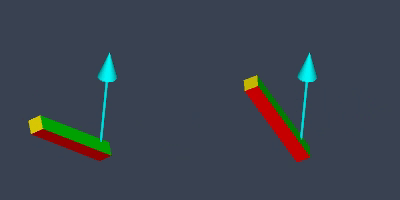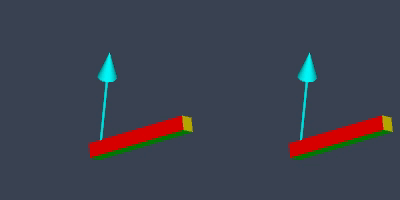
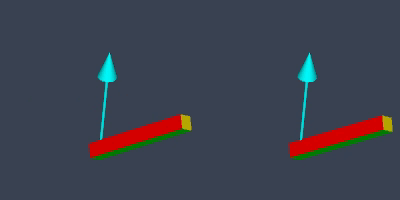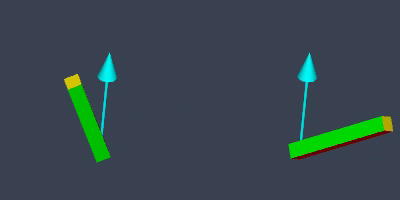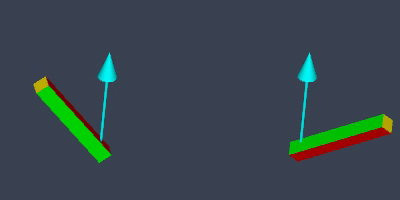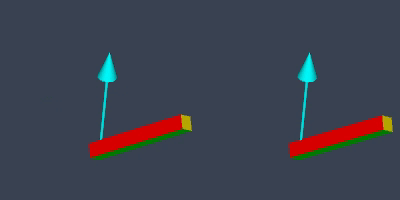
If we slerp between the two orientations, this is what we get:

Mathematically, slerp takes the “shortest rotational path”. The quaternion representing the rod’s orientation travels along the shortest arc on a 4D hyper sphere. But, given the rod’s elongated appearance, the rod’s moving end seems to be deviating from the shortest arc on a 3D sphere.

My intended effect here is for the rod’s moving end to travel along the shortest arc in 3D, like this:

The difference is more obvious if we compare them side-by-side:

This is where swing-twist decomposition comes in.

Swing-Twist Decomposition

Swing-Twist decomposition is an operation that splits a rotation into two concatenated rotations, swing and twist. Given a twist axis, we would like to separate out the portion of a rotation that contributes to the twist around this axis, and what’s left behind is the remaining swing portion.

There are multiple ways to derive the formulas, but this particular one by Michaele Norel seems to be the most elegant and efficient, and it’s the only one I’ve come across that does not involve any use of trigonometry functions. I will first show the formulas now and then paraphrase his proof later:

public static void DecomposeSwingTwist
(
  Quaternion q, 
  Vector3 twistAxis, 
  out Quaternion swing, 
  out Quaternion twist
)
{
  Vector3 r = new Vector3(q.x, q.y, q.z);
 
  // singularity: rotation by 180 degree
  if (r.sqrMagnitude < MathUtil.Epsilon)
  {
    Vector3 rotatedTwistAxis = q * twistAxis;
    Vector3 swingAxis = 
      Vector3.Cross(twistAxis, rotatedTwistAxis);
 
    if (swingAxis.sqrMagnitude > MathUtil.Epsilon)
    {
      float swingAngle = 
        Vector3.Angle(twistAxis, rotatedTwistAxis);
      swing = Quaternion.AngleAxis(swingAngle, swingAxis);
    }
    else
    {
      // more singularity: 
      // rotation axis parallel to twist axis
      swing = Quaternion.identity; // no swing
    }
 
    // always twist 180 degree on singularity
    twist = Quaternion.AngleAxis(180.0f, twistAxis);
    return;
  }
 
  // meat of swing-twist decomposition
  Vector3 p = Vector3.Project(r, twistAxis);
  twist = new Quaternion(p.x, p.y, p.z, q.w);
  twist = Normalize(twist);
  swing = q * Quaternion.Inverse(twist);
}

Now that we have the means to decompose a rotation into swing and twist components, we need a way to use them to interpolate the rod’s orientation, replacing slerp.

Swing-Twist Interpolation

And as we concatenate these two components together, we get a swing-twist interpolation that rotates the rod such that its moving end travels in the shortest arc in 3D. Again, here is a side-by-side comparison of slerp (left) and swing-twist interpolation (right):

I decided to name my swing-twist interpolation function sterp. I think it’s cool because it sounds like it belongs to the function family of lerp and slerp. Here’s to hoping that this name catches on.

And here’s my code implementation:

public static Quaternion Sterp
(
  Quaternion a, 
  Quaternion b, 
  Vector3 twistAxis, 
  float t
)
{
  Quaternion deltaRotation = b * Quaternion.Inverse(a);
   
  Quaternion swingFull;
  Quaternion twistFull;
  QuaternionUtil.DecomposeSwingTwist
  (
    deltaRotation, 
    twistAxis, 
    out swingFull, 
    out twistFull
  );
 
  Quaternion swing = 
    Quaternion.Slerp(Quaternion.identity, swingFull, t);
  Quaternion twist = 
    Quaternion.Slerp(Quaternion.identity, twistFull, t);
 
  return twist * swing;
}

Proof

Conclusion

That’s all.

Given a twist axis, I have shown how to decompose a rotation into a swing component and a twist component.

Such decomposition can be used for swing-twist interpolation, an alternative to slerp that interpolates between two orientations, which can be useful if you’d like some point on a rotating object to travel along the shortest arc.

I like to call such interpolation sterp.

Sterp is merely an alternative to slerp, not a replacement. Also, slerp is definitely more efficient than sterp. Most of the time slerp should work just fine, but if you find unwanted orientational sway on an object’s moving end, you might want to give sterp a try.

Interesting, but I wonder about the example and possible generalizations.

• You choose the the rod's axis as the twist axis, which looks good in the example, but what twist axis is best in less obvious cases? For instance, rotating a cube.
• Decomposing the full rotation R as R=S*T and interpolating S and T separately obviously generalizes to splitting R into a product of three or more rotations and to interpolating the rotations at different variable speeds. For example, mechanical parts could do all or most swing before braking hard and beginning the twist (probably a much "smaller" movement).

I would say it depends on your intended look.
As a general fallback, maybe align the twist axis with the direction in which the object's vertices are most spread out using techniques like PCA (principal component analysis), or simply the longest side of the object's OBB?

As for the mechanical example, you gave a good example of where spliting the swing and twist portions in time is even more desirable. In this case, maybe a version of sterp that takes separate swing and twist interpolation parameters can be useful? Or if full control is needed, simply use the raw swing and twist from the decomposition function.

public static Quaternion Sterp
(
  Quaternion a, 
  Quaternion b, 
  Vector3 twistAxis, 
  float tSwing, 
  float tTwist
)
{
  Quaternion deltaRotation = b * Quaternion.Inverse(a);
   
  Quaternion swingFull;
  Quaternion twistFull;
  QuaternionUtil.DecomposeSwingTwist
  (
    deltaRotation, 
    twistAxis, 
    out swingFull, 
    out twistFull
  );
 
  Quaternion swing = 
    Quaternion.Slerp(Quaternion.identity, swingFull, tSwing);
  Quaternion twist = 
    Quaternion.Slerp(Quaternion.identity, twistFull, tTwist);
 
  return twist * swing;
}